Solving Number Workout using an SMT (integer) solver

Continuing the series of solving puzzles using an integer SMT solver we look now at the Number workout puzzle. This number placement puzzle is published in the Daily Mail weekend TV supplement. The puzzle offers a hexagonal grid sub-divided with each hexagon subdivided into six regions into which sequential numbers ( 1..6 ) must be placed. Some initial clue numbers are provided. The numbers must be unique within the regions and where the regions touch must have the same value.

Encoding

The puzzle is encoded into text then a script is used to generate the underlying logic of the puzzle. These logic lines are then passed to an SMT solver for analysis and resolution. Microsoft's Z3 and MathSAT solvers are used. The thirteen hexagons are fixed across the grid. The clue cell locations can be determined from the encoded input. Single digit integers are used for the input with 0 for unknown and number for a clue cell.

#nw nw_003.txt DMWeekend 25 May 2020

501

040000050

100000002

200006003

000000000

400600005

000003006

300200006

060000040

401

Puzzle Logic

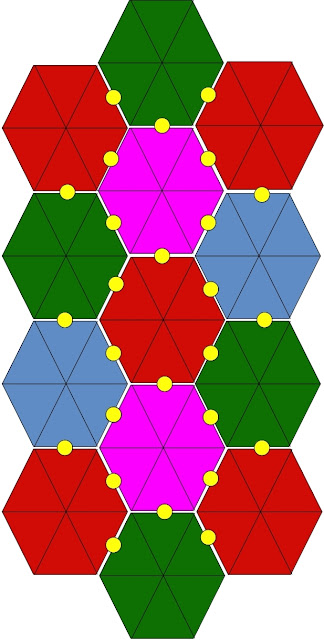Fig 1: Number Workout grid showing yellow spots on boundary cell pairs

The logic of the puzzle breaks down in to two main sets of constraints. Firstly the hexagon regions have unique numbers ( 1 .. 6 ) and values on adjacent hexagon boundaries must be the same. Some clue numbers are provided. 

This puzzle resembles Hidato for a neighbour cell constraints and Sudoku for the region values constraints. However the hexagon grid layout and boundary neighbour cells equality constraints make this puzzle unique.

The common boundary cell constraint provides considerable leverage in solving the puzzle and could be handled in two ways. Either the second cell is ignored and the boundary cells are encoded to appear in both hexagon groups or all cells are used with an equality rule generated. Both methods require knowing which pairs of cells in the input are on a hexagon boundary.

Neighbouring boundary cells

Three possible methods for identifying boundary cells were considered :

1. Geometry - Each cell position is calculated and when the distance between any two cells is a specific value they would be declared as neighbour cells.
2. Cell region map - The grid is fixed and the input cell order is fixed therefore an input map could be used to identify cell pairs.
3. Counting - If the cells are counted in rows (from one) then these rules would identify the cell pairs: 

•  "The third and forth cell on each row" and 
•  "The sixth and seventh cell on each row" and
•  "The fifth cell on even rows is the pair of the fifth cell on the next row down" and 
•  "The second and eighth cells on odd rows are paired with the same cells on the next row"

The first method was considered but was considered overly complex for this size puzzle. The third method was considered the most adaptable to variable grid sizes but somewhat complex to code and check. 

Both first and third methods would be used to build a cell region map (as per method 2), but as the puzzle has only been seen in a single size, directly generating the cell region map seemed reasonable. If other shapes and sizes of this puzzle are seen then the region map could be dynamically built using methods 1 or 3. 

For this solution a region map was directly built and encoded in rows as a follows :

#NumberWorkout Cell mapping by groups "This input cell is in these hexagon groups" Groups must be in ascending order

@nwMapGroups = (

["1","1","1"],

["2","2",  "1 2","1 2","1 4", "1 3","1 3","3","3"],

["2","2 5","2 4","2 4","1 4", "3 4","3 4","3 6","3"],

["5","2 5","4 5","4 5","4 7", "4 6","4 6","3 6","6"],

["5","5 8","5 7","5 7","4 7", "6 7","6 7","6 9","6"],

["8","5 8","7 8","7 8","7 10","7 9","7 9","6 9","9"],

["8","8 11","8 10","8 10","7 10","9 10","9 10","9 12","9"],

["11","8 11","10 11","10 11","10 13","10 12","10 12","9 12","12"],

["11","11","11 13","11 13","10 13","12 13","12 13","12","12"],

["13","13","13"]

);

By using the row structure of the puzzle each input cell has one or two hexagon region numbers identified. For example in the second cell on row three is "2 5" meaning this cell is in hex regions 2 and 5. In this map the regions for each cell must be listed in lower value first to ensure cell pairs can be found.  As there is only one common boundary between pairs of regions using the region number pairs in order is enough to bring together neighbour cell pairs.  

For example "11 13","11 13"  identifies the two cells in hex regions 11 & 13 that are neighbours.  As the puzzle is read in specific internal group and cell numbers are generated with a pairs list constructed simultaneously for the 13 hexagon regions. 

Clue numbers that appear in one of a region boundary pair have to be propagated to the other cell in the pair. The equivalence constraint could be dropped for a region pair that both have set values but the resulting redundant logic does not appear to impact the solution time for puzzles of this size.

#->grpList cell values = 

1 = 0 1 2 5 7 8 !

2 = 3 4 5 12 13 14 !

3 = 8 10 11 17 19 20 !

4 = 7 14 17 23 25 26 !

5 = 13 21 23 30 31 32 !

6 = 19 26 29 35 37 38 !

7 = 25 32 35 41 43 44 !

8 = 31 39 41 48 49 50 !

9 = 37 44 47 53 55 56 !

10 = 43 50 53 59 61 62 !

11 = 49 57 59 66 67 68 !

12 = 55 62 65 71 73 74 !

13 = 61 68 71 75 76 77 !

#->pairs cell values = 5 6 ! 7 16 ! 8 9 ! 14 15 ! 13 22 ! 17 18 ! 19 28 ! 23 24 ! 26 27 ! 25 34 ! 31 40 ! 32 33 ! 35 36 ! 37 46 ! 41 42 ! 43 52 ! 44 45 ! 50 51 ! 49 58 ! 53 54 ! 55 64 ! 61 70 ! 62 63 ! 59 60 ! 68 69 ! 71 72 !

To obtain the solution the solver only needs to know the value range and relationships between cells. Nothing about the physical positions of cells and regions is required for successful encoding.

Building SMT-LIB file

After the usual preamble an Int variable is set for each of the 78 cells. 

(set-logic LIA)

(set-option :produce-models true)

(set-option :produce-assignments true)

(declare-const V0 Int)

(declare-const V1 Int)

(declare-const V2 Int)

....

(declare-const V77 Int)

The value range for every cell is set as 1 .. 6

(assert (and (> V0 0) (< V0 7) ))

(assert (and (> V1 0) (< V1 7) ))

(assert (and (> V2 0) (< V2 7) ))

(assert (and (> V3 0) (< V3 7) ))

....

(assert (and (> V77 0) (< V77 7) ))

The clue cells values are assigned

(assert (= V0 5 ))

(assert (= V2 1 ))

(assert (= V4 4 ))

.....

(assert (= V75 4 ))

(assert (= V77 1 ))

The hex regions are built from the grpList structure

(assert (distinct V0 V1 V2 V5 V7 V8)) ; Region 1

(assert (distinct V3 V4 V5 V12 V13 V14)) ; Region 2

.....

(assert (distinct V61 V68 V71 V75 V76 V77)) ; Region 13

Finally the boundary cells are set for equality

(assert (= V5 V6 ))

(assert (= V7 V16 ))

(assert (= V8 V9 ))

(assert (= V14 V15 ))

(assert (= V13 V22 ))

.....

If the puzzle can be solved the output would be "sat" followed by the values for each square. The solver takes about 0.09s on a MacBookPro 2011 with a 2.2Ghz Core i7

$ ./numberWorkout.pl < nw_003.txt | time ../solver_m5

sat

( (V0 5)

  (V1 4)

  (V2 1)

  (V3 2)

  (V4 4)

.....

  (V75 4)

  (V76 2)

  (V77 1) )

Displaying the output

The usual technique of reading the solver output back into the logic generation script for display and checking is used. However the output generation for this puzzle varies from a standard rectangular grid as used by Sudoku, Hidato and similar puzzles.  For this puzzle a different method of placing the results on top of an image of the input grid was required. See appendix below for more details.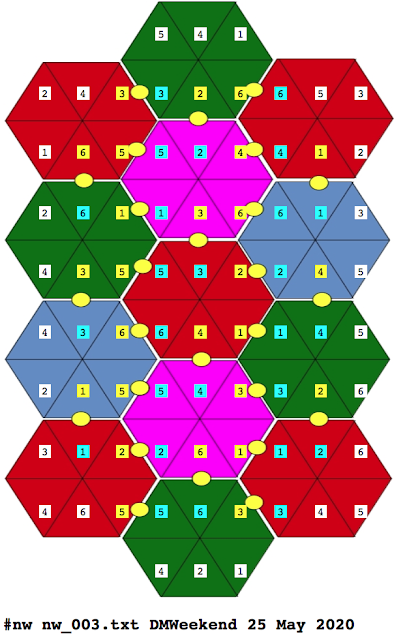 

The result image is generated with the pairs of boundary cells highlighted in yellow and teal.

Fig:2 the solved puzzle, Yellow cells are "First of Pair", Teal are "Last Of Pair"

The checking lines show that the hexagon regions and number pairs are correct.

#nw nw_003.txt DMWeekend 25 May 2020

Checking Neighbour pairs = Cell 5 6 = ( 3=?=3 ) OK Cell 7 16 = ( 2=?=2 ) OK Cell 8 9 = ( 6=?=6 ) OK Cell 13 22 = ( 6=?=6 ) OK Cell 14 15 = ( 5=?=5 ) OK Cell 17 18 = ( 4=?=4 ) OK Cell 19 28 = ( 1=?=1 ) OK Cell 25 34 = ( 3=?=3 ) OK Cell 23 24 = ( 1=?=1 ) OK Cell 26 27 = ( 6=?=6 ) OK Cell 32 33 = ( 5=?=5 ) OK Cell 31 40 = ( 3=?=3 ) OK Cell 37 46 = ( 4=?=4 ) OK Cell 35 36 = ( 2=?=2 ) OK Cell 44 45 = ( 1=?=1 ) OK Cell 43 52 = ( 4=?=4 ) OK Cell 41 42 = ( 6=?=6 ) OK Cell 50 51 = ( 5=?=5 ) OK Cell 49 58 = ( 1=?=1 ) OK Cell 55 64 = ( 2=?=2 ) OK Cell 53 54 = ( 3=?=3 ) OK Cell 59 60 = ( 2=?=2 ) OK Cell 61 70 = ( 6=?=6 ) OK Cell 62 63 = ( 1=?=1 ) OK Cell 68 69 = ( 5=?=5 ) OK Cell 71 72 = ( 3=?=3 ) OK 

Checking Hex Regions =
Region 1 Cells are 0 1 2 5 7 8 OK
Region 2 Cells are 3 4 5 12 13 14 OK
Region 3 Cells are 8 10 11 17 19 20 OK
Region 4 Cells are 7 14 17 23 25 26 OK
Region 5 Cells are 13 21 23 30 31 32 OK
Region 6 Cells are 19 26 29 35 37 38 OK
Region 7 Cells are 25 32 35 41 43 44 OK
Region 8 Cells are 31 39 41 48 49 50 OK
Region 9 Cells are 37 44 47 53 55 56 OK
Region 10 Cells are 43 50 53 59 61 62 OK
Region 11 Cells are 49 57 59 66 67 68 OK
Region 12 Cells are 55 62 65 71 73 74 OK
Region 13 Cells are 61 68 71 75 76 77 OK 
Puzzle has is OK Solution successful.

Error checks test 

If another puzzle is taken and the results from the solver adjusted before display the error checks should show that cell in fifth row has a incorrect value.

 cat nw_001M5.res | sed 's/V35 2/V35 4/' | ./numberWorkout.pl -f nw_001.txt > nw_001BROKEN.html

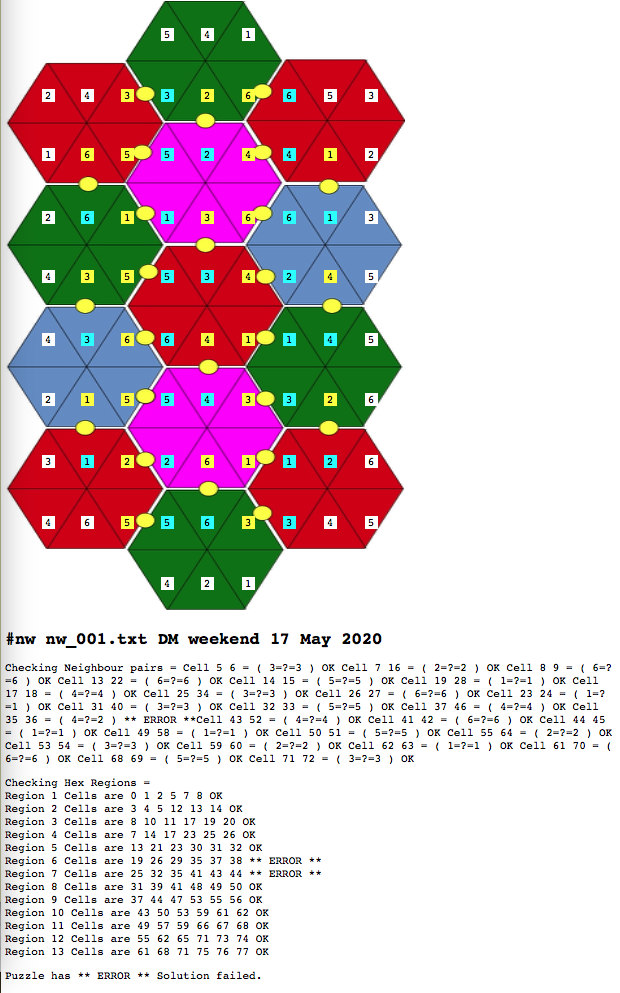Fig 3: Introducing an error into the solver output to show solution error checking

Usage for logic preparation script

Usage: NumberWorkout {options} < puzzle.txt  or

    NumberWorkout {options} -f puzzle.txt < SolverOutput

    -v N :Be verbose to level N ( use v=10 for detailed output )

    -f puzzle.txt :Puzzle file needed when reading Solver output use STDIN otherwise

    

    Programs reads STDIN looking for either puzzleFile format lines or Solver output lines

        If the input is in puzzleFile format the program will generate solver input lines.

        If the input is in Solver output lines format the program will expect a -f puzzleFile paremeter.

            Using both these input streams program will then generate display .html output.

Game Rules

13 segmented hexagons are stacked with aligned segments. 1..6 must be put in the segments of the hegagons such that where the segemnts are aligned the number in those segments must be the same. No duplicates in a single segment. Edges must match.

Stack of hexagons ..

 *

* *

 *

* *

 *

Encode NumberWorkout puzzle Input as follows, 0 for unknown and clue numbers included.

    Error Template violation is given if not 3 or 9 numbers on an input line

        

    $ cat nw_001.txt

    #NW_001.txt DM weekend 17 May 2020

    501

    040000050

    100000002

    200000003

    000000000

    400600005

    000003006

    300200006

    060000040

    401

OR Process results from solver in the following format

    sat

    ( (V0 9)

    (V1 7)

    (V2 5)

    (V3 3)

    ....

to generate an html layout as output.

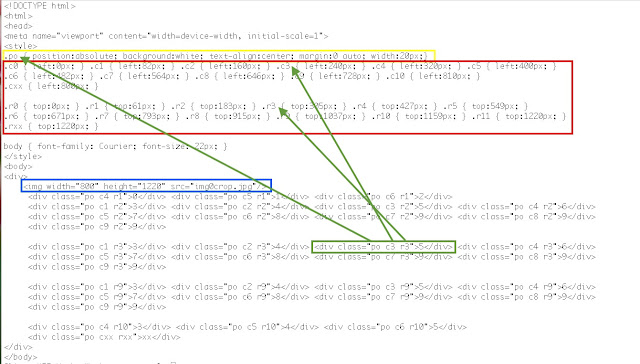
Appendix  : Placing tags on an image using CSS formatting

Creating the output image for the puzzle turned out to be quite simple but rather fiddly. After some trial and lots of error, a simple way to overlay an image with tags was used.  The output image is assembled into a web page and then displayed in a standard browser. The resulting webpage is then printed to a file using a screenshot utility or print to .pdf function.

Fig 4 Shows the parts required to build the tags over image web display page.

The style section of the page defines how certain elements are to look.  po in yellow box sets the format for a tag. Then c0 to cxx, in red box, define the column positions followed by r0 to rxx the definitions for the row positions.

The image is displayed in the blue box. The tags are then individually placed using the class string built from the above styles. The example in green box "po c3 r3" is positioned at from left 240px and from top 305px.

For the results image the styes py and pb where added along side p0 with definitions that included a different  background:colour; definitions.

Fig4: Webpage elements for Tags over image

Using CSS tags to annotate an image is preferable to overlaying an html table because the tags can be generated in any order. The whole html result document can be generated by the script with adjusted image size and column and row placements if required. 

Acknowledgments

Thanks to w3schools for the CSS tutorial information and Design Consideration for the useful blog entry.

Solving Suguru using an SMT (integer) solver

Continuing the series of solving puzzles using an integer SMT solver we look now at the Suguru puzzle. This popular number placement puzzle is published in the Daily Mail newspaper and other publications. The puzzle offers a variable size rectangular grid sub-divided into regions into which sequential numbers ( 1.. region size) must be placed. Some initial clue numbers are provided. The numbers must be unique within the regions and each cell must not touch (kings move) any other cell with the same value.

Suguru puzzle 6 by 6

Encoding

The puzzle is encoded into text then a script is used to generate the underlying logic of the puzzle. These logic lines are then passed to an SMT solver for analysis and resolution. Microsoft's Z3 and MathSAT solvers are used. A region letter is used for each cell followed by a clue number if provided.

#Suguru Page59 DR  su_002.txt

a,b,b,b,b,c

a,a4,d,c3,c,c

a,d,d,d,e5,c

f,f2,d,g,e,e

h,f,g,g,g,e2

h,f,f,g,i,e

Puzzle Logic

The logic of the puzzle breaks down in to two main sets of constraints. Firstly the regions have to have ascending numbers and secondly adjoining cell values must differ.  Some clue numbers are provided. A single cell region must have the value 1 see above ( region i, the fifth cell along the bottom row ).

This puzzle resembles Hidato for a neighbour cell constraints and KenKen for the region values constraints.

After the usual preamble an Int variable is set for each cell

(set-logic UFNIA)

(set-option :produce-models true)

(set-option :produce-assignments true)

(declare-const V0 Int)

(declare-const V1 Int)

(declare-const V2 Int)

.... up to cell V35

(declare-const V35 Int)

As the region sizes have been analysed during input we can set constrains for each cell based on the number of cells in the region.

(assert (and (>= V0 1) (<= V0 4)))

(assert (and (>= V1 1) (<= V1 4)))

(assert (and (>= V2 1) (<= V2 4)))

(assert (and (>= V3 1) (<= V3 4)))

(assert (and (>= V4 1) (<= V4 4)))

(assert (and (>= V5 1) (<= V5 5))) ; Region c

(assert (and (>= V6 1) (<= V6 4)))

.... up to cell V35

The clue numbers are set ....

(assert (= V7 4 ))

(assert (= V9 3 ))

(assert (= V16 5 ))

(assert (= V19 2 ))

(assert (= V29 2 ))

The region numbers are set .... to be distinct values ..

(assert (distinct V0 V6 V7 V12)) ; Region a

(assert (distinct V1 V2 V3 V4)) ; Region b

(assert (distinct V5 V9 V10 V11 V17)) ; Region c

(assert (distinct V8 V13 V14 V15 V20)) ; Region d

(assert (distinct V16 V22 V23 V29 V35)) ; Region e

(assert (distinct V18 V19 V25 V31 V32)) ; Region f

(assert (distinct V21 V26 V27 V28 V33)) ; Region g

(assert (distinct V24 V30)) ; Region h

Except for single cell region that is just set to a clue number 1.

(assert (= V34  1)); Region i Single cell

Neighbour cells

Finding the neighbours for each cell is the interesting part for this puzzle. Sequential cell numbers are used and the width (w) of the puzzle is known. In the centre of the puzzle, for the clue in cell 9 we can find its neighbours by +/- w and +/- 1. 

The following are the addresses of the neighbours of cell 9

[ 9 -w -1 ]  [ 9 -w ]  [ 9 -w +1]  [9 -1]  [9+1]  [ 9 +w -1 ]  [ 9 -w ]  [ 9 +w +1]

  

Suguru Grid size 6 Neighbours of 9

giving cell numbers 2,3,4,8,10,14,15,16 and producing the the logic line 

(assert (and  

(not (= V9 V2)) (not (= V9 V3)) (not (= V9 V4)) 

(not (= V9 V8)) (not (= V9 V10)) 

(not (= V9 V14)) (not (= V9 V15)) (not (= V9 V16)

))); Neighbours of 9

However for the cells along the edges and in the corner of the puzzle the neighbour cell generation has to avoid falling of the edge of the puzzle. Also sequential cells are not necessarily neighbours see cell 11 is not a neighbour of cell 12. The corners only have 3 neighbours and cells along the side only 5 neighbours. 

To find the correct neighbours of a cell we calculate all the possible neighbours then filter out the non-neighbour and off the edge cells.

 @nlist = ( $cell-1-$w, $cell-0-$w, $cell+1-$w, $cell-1,$cell+1, 

            $cell-1+$w, $cell-0+$w, $cell+1+$w );

 foreach $i ( @nlist )

     {  $res .= "V$i " 

        unless ( ( $i < 0 ) or ( $i > $last) or 

               ( abs( $i % $w - $cell % $w ) > 1 ) )

     };

The unless clause here has the key tests, first cells address below 0 and cells beyond the last possible address are excluded then critically the absolute column distance between the cells is checked. The modulus operator % gives the remainder after dividing the cell addresses in $i and $cell by the width of the board in $w.  The abs function flips -ve numbers positive. If the subtraction result is more than 1 then the cells are not neighbours.  Trying this on cell 11 with cells 10 and 12. For cell 10 we get  abs( 11 % 6  - 10 % 6 ) = abs ( 5 - 4 ) = 1 therefore cell 10 is a neighbour of 11. For cell 12 we get  abs( 11 % 6  - 12 % 6 ) = abs( 5 - 0 ) = 5 therefore cell 12 is not a neighbour of 11. 

All the cell neighbours are calculated in the same way resulting in the logic lines for cell neighbour constraints.

(assert (and  (not (= V0 V1)) (not (= V0 V6)) (not (= V0 V7)))); Neighbours of 0

(assert (and  (not (= V1 V0)) (not (= V1 V2)) (not (= V1 V6)) 

(not (= V1 V7)) (not (= V1 V8)))); Neighbours of 1

........

(assert (and  (not (= V6 V0)) (not (= V6 V1)) (not (= V6 V7)) 

(not (= V6 V12)) (not (= V6 V13)))); Neighbours of 6

........

(assert (and  (not (= V8 V1)) (not (= V8 V2)) (not (= V8 V3)) (not (= V8 V7)) (not (= V8 V9)) (not (= V8 V13)) (not (= V8 V14)) (not (= V8 V15)))); Neighbours of 8

This is the more mundane approach of finding neighbour cells. In other puzzles eg Hidato  a grid bigger than the game board is used with off edge cells being neutral.

Results

As with the previous puzzles the logic generating script was coded to read in the solvers output and then generate output using the original puzzle and check the answers provided. Using display colours helps identify the cells of a region. 

Suguru completed showing regions and values with result check lines

Error checks test 

If another puzzle is taken and the results from the solver adjusted before display the error checks should show that cell 7 has a duplicate value.

$ perl ./suguru_smt2.pl < su_001.txt | ../solver_m5 | sed '/V7/s/4/3/' | ./suguru_smt2.pl -f su_001.txt > su_001BROKEN.html 

Suguru showing error detection for cells 3,7,8 and region b

Appendix Script Usage

A script is used to generate the logic lines from the encoded puzzle and subsequently read the solver output and generate the results display.

Usage: Suguru {options} < puzzle.txt  or

    Suguru {options} -f puzzle.txt < SolverOutput

    -v N :Be verbose to level N ( use v=1 for detailed output )

    -f puzzle.txt :Puzzle file needed when reading Solver output use STDIN otherwise

    

    Programs reads STDIN looking for either puzzleFile format lines or Solver output lines

        If the input is in puzzleFile format the program will generate solver input lines.

        If the input is in Solver output lines format the program will expect a -f puzzleFile paremeter.

            Using both these input streams program will then generate display .html output.

Game Rules

Each regions has cells set from 1 .. N where N is size of region. Repeats NOT allowed in any region.

Encoding Rules

Each cell belongs to a single region/cage. Regions must be uniquely filled with 1..N.

No bordering cells (kings move) can have the same number. Clue numbers are pre-place in some cells.

Single empty cell regions are 1.

Region names must be unique.

Typically puzzles are square and have 5 or 6 cells but not neccessarly

    Numbers may not repeat with a region or on adjcent cells.

Each Suguru puzzle Input as follows each caged squares must belong to a region

        region_lable{Value}{operation+-*/}

        

     su_001.txt

    #Suguru Number 60 DR  su_001.txt

    a,a,b,c,c

    a,b,b,b,c2

    a2,d5,c,e1,c

    a,d,e,e,c

    d,d,d,e4,e

to generate an SMT2 input file. Use a .. z and A .. Z or aa .. zz for region/cage names

OR Process results from solver in the following format

    sat

    ( (V0 9)

    (V1 7)

    (V2 5)

    (V3 3)

    ....

to generate an html table as output