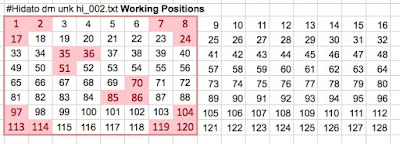
Looking at this xmas gift wooden puzzle it seems like it would be a good candidate for an SMT (integer) solver solution. The 19 blocks have to be arranged in the frame in such a way that the tile numbers on each of the blue, orange and green lines add up to 38.
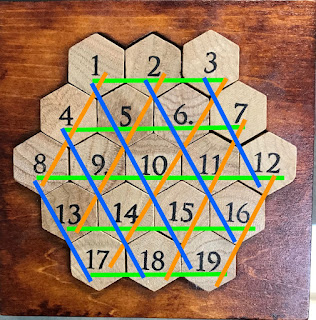
These logic lines represent the puzzle in a way that a general purpose solver can digest.
Preamble set the solve win to integer mode.
(set-logic LIA)
(set-option :produce-models true)
(set-option :produce-assignments true)
Each of the 19 slots is defined as an integer V1 to V19 that can have the value 1..19
(declare-const V1 Int)
(assert ( and (>= V1 1 ) (<= V1 19)) )
(declare-const V2 Int)
(assert ( and (>= V2 1 ) (<= V2 19)) )
(declare-const V3 Int)
(assert ( and (>= V3 1 ) (<= V3 19)) )
(declare-const V4 Int)
(assert ( and (>= V4 1 ) (<= V4 19)) )
(declare-const V5 Int)
(assert ( and (>= V5 1 ) (<= V5 19)) )
(declare-const V6 Int)
......
(assert ( and (>= V14 1 ) (<= V14 19)) )
(declare-const V15 Int)
(assert ( and (>= V15 1 ) (<= V15 19)) )
(declare-const V16 Int)
(assert ( and (>= V16 1 ) (<= V16 19)) )
(declare-const V17 Int)
(assert ( and (>= V17 1 ) (<= V17 19)) )
(declare-const V18 Int)
(assert ( and (>= V18 1 ) (<= V18 19)) )
(declare-const V19 Int)
(assert ( and (>= V19 1 ) (<= V19 19)) )
Each slot must have it's own distinct value.
(assert (distinct V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 V16 V17 V18 V19))
These constraints represent the 15 lines that have to add up to 38.
(assert (= 38 (+ V1 V2 V3 )))
(assert (= 38 (+ V4 V5 V6 V7 )))
(assert (= 38 (+ V8 V9 V10 V11 V12 )))
(assert (= 38 (+ V13 V14 V15 V16 )))
(assert (= 38 (+ V17 V18 V19 )))
(assert (= 38 (+ V1 V8 V4 )))
(assert (= 38 (+ V2 V5 V9 V13 )))
(assert (= 38 (+ V3 V6 V10 V14 V17 )))
(assert (= 38 (+ V7 V11 V15 V18 )))
(assert (= 38 (+ V12 V16 V19 )))
(assert (= 38 (+ V8 V13 V17 )))
(assert (= 38 (+ V4 V9 V14 V18 )))
(assert (= 38 (+ V1 V5 V10 V15 V19 )))
(assert (= 38 (+ V2 V6 V11 V16 )))
(assert (= 38 (+ V3 V7 V12 )))
Post amble to trigger the solver and display the answers
(check-sat)
(get-model)
(exit)
Run the logic lines into a solver then load the answers into a spreadsheet to check the answers.
$ ./hex38.pl | time ../solver_m5
sat
( (V1 9)
(V2 14)
(V3 15)
(V4 11)
(V5 6)
(V6 8)
(V7 13)
(V8 18)
(V9 1)
(V10 5)
(V11 4)
(V12 10)
(V13 17)
(V14 7)
(V15 2)
(V16 12)
(V17 3)
(V18 19)
(V19 16) )
2.75 real 2.66 user 0.02 sys
The MathSat solver takes a 2.75s, the Z3 solver 1.2s to run on a MacBook Pro i7.
The above answers and the two shown below are reversed/reflected but are identical.
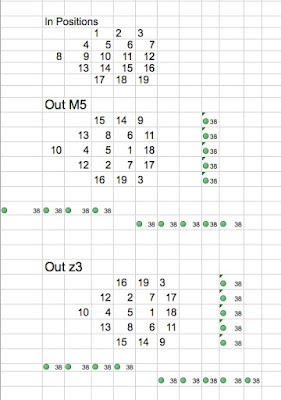
Display the answer ...

Perl script to generate the Solver logic lines
# create the hex38 smt2 lines
#
print "(set-logic LIA)\n(set-option :produce-models true)\n(set-option :produce-assignments true)\n";
for $i (1..19) {
print "(declare-const V$i Int)\n" ;
print "(assert ( and (>= V$i 1 ) (<= V$i 19)) )\n" };
print "(assert (distinct";
for $i (1..19) { print " V$i"};
print "))\n";
@deps = (
[1, 2, 3], [4, 5, 6, 7], [8, 9, 10, 11, 12], [13, 14, 15, 16], [17, 18, 19],
[1, 8, 4], [2, 5, 9, 13], [3, 6, 10, 14, 17], [7, 11, 15, 18], [12, 16, 19], [8, 13, 17],
[4, 9, 14, 18], [1, 5, 10, 15, 19], [2, 6, 11, 16], [3, 7, 12]
);
foreach $i ( @deps )
{
print "(assert (= 38 (+ " ;
map { print "V$_ "} @$i;
print ")))\n" ;
}
print "(check-sat)\n(get-model)\n(exit)\n";