Solving Kakuro using an SMT (Integer) solver

Continuing in the short series of reframing puzzles and using an SMT integer solver to find a solution we look now at solving the Kakuro class of problem.  This popular number placement puzzle seen in the UK papers Daily Telegraph and Daily Mail. This puzzle is similar to Sudoku using a rectangular grid of numbers but differs in that target sums are set for horizontal and vertical lines. The numbers 1..9 are placed in the grid such that the sum of the numbers equals the target provided. Any number can only used once in each horizontal and vertical sum.

Looking at the incorrectly completed Kakuro diagram below the blue numbers are the answer cells which would be all blank at the start of the puzzle. The green cells are the target sums annotated as "down \ across". The red cells are targets that are not correctly answered. For example on the top row 4\ represents the vertical target sum for the two cells below. As 1+2 = 3 this is not the answer of 4 that we are after.  Also the horizontal part of the target sum 15\14 adds up to 13. The other constraint is that any of the digits 0 to 9 can appear only once in a sum. To make total 4 the digits 1 and 3 must be used.

Incorrectly completed Kakuro

This puzzle can be prepared for an integer solver by transforming the input puzzle and generating the required propositional SMT-LIB input lines. Starting with the text format of the puzzle as follows:

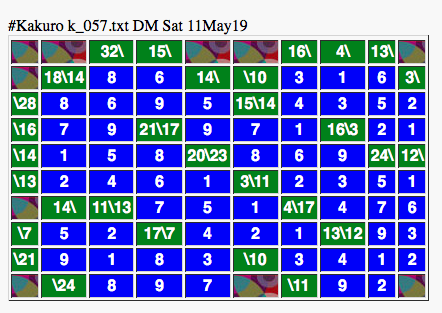
#Kakuro k_057.txt DM Sat 11May19

x,x,32\,15\,x,x,16\,4\,13\,x

x,18\14,0,0,14\,\10,0,0,0,3\

\28,0,0,0,0,15\14,0,0,0,0

\16,0,0,21\17,0,0,0,16\3,0,0

\14,0,0,0,20\23,0,0,0,24\,12\

\13,0,0,0,0,3\11,0,0,0,0

x,14\,11\13,0,0,0,4\17,0,0,0

\7,0,0,17\7,0,0,0,13\12,0,0

\21,0,0,0,0,\10,0,0,0,0

x,\24,0,0,0,x,\11,0,0,x

Each cell is identified as either a block "X", answer cell "0" or target cell with one or two target sums.  For each of the answer cells we declare an int and set a range.

(declare-const V12 Int)

(declare-const V13 Int)

(declare-const V16 Int)

...

(assert (and (> V12 0) (< V12 10)))

(assert (and (> V13 0) (< V13 10)))

(assert (and (> V16 0) (< V16 10)))

...

The slightly tricky bit is generating the target sums and setting the parts of that sum to have unique cell answers. This is achieved by generating a list of the cells involved with each target sum. For Example in cell 11 we have 18\14 that splits into target sums "H11" & "V11".  H11 is the sum of cells 12,13 which must be 14 and V11 is the sum of cells 21,31,41,51 which must be 18.

# H11,12,13 is 14

# H15,16,17,18 is 10

# H20,21,22,23,24 is 28

.....

# V11,21,31,41,51 is 18

# V14,24,34 is 14

# V19,29,39 is 3

These are reformatted into the propositional logic lines.... two lines for each equation to see the sum and insist on the uniqueness of the involved cells.

(assert (= 14 (+ V12 V13 )))

(assert (distinct V12 V13 ))

(assert (= 10 (+ V16 V17 V18 )))

(assert (distinct V16 V17 V18 ))

(assert (= 28 (+ V21 V22 V23 V24 )))

...

(assert (= 18 (+ V21 V31 V41 V51 )))

(assert (distinct V21 V31 V41 V51 ))

Along with some supporting lines this is all fed into the solver that generates an answer for each cell.  The solver for this puzzle takes 0.08s on a MacBook Pro 2.2Hz.

$ ../solver_m5 <  k_057.txt.sml

sat

( (V12 8)

  (V13 6)

  (V16 3)

  (V17 1)

  (V18 6)

  (V21 8)

  (V22 6)

.....

A script is used to generate the solver lines from the puzzle and re-used to read the answers from the solver to generate the html format for the output picture. The script also checks the answers and colours the target sum cells red if a failure is detected.  The correct answer, as provided by the solver, is shown here.

$ ./kakuro_SMT2.pl <  samples/k_057.txt  | ../solver_m5 | ./kakuro_SMT2.pl -f samples/k_057.txt  > k_057.html 

We could have helped the solver by narrowing the range of each answer cell. For example to make the target sum 17 with two numbers only 8 and 9 are candidates for the answer cells.  Adjusting the lines

(assert (and (> V87 0) (< V87 10)))

(assert (and (> V97 0) (< V97 10)))

to

(assert (and (> V87 7) (< V87 10)))

(assert (and (> V97 7) (< V97 10)))

would have narrowed the work needed by the solver but given the puzzle runtime of under 0.09s this was not considered necessary.

Kakuro table

This table shows the number of choices available for filling target lines of a given length with a given sum. For Example there are 42 ways to make Target 18 using 3 sequence digits.

$ Use_tables.pl -i 3,18

Entry [3,18] = 189 198 279 297 369 378 387 396 459 468 486 495 549 567 576 594 639 648 657 675 684 693 729 738 756 765 783 792 819 837 846 864 873 891 918 927 936 945 954 963 972 981

Kakuro count table

Solving Classic and other Sudoku using an SMT (Integer) solver.

Standard 9*9 Sudoku, Hard example.

Sudoku is a popular recreational puzzle comprising a 9 by 9 grid of numbers all in the range 1..9. The puzzle must be completed whilst observing the simple rule that no number can be repeated in any row, column or the outlined 3*3 sub square by extension every row, column and sub square must have each of the digits 1..9. 

In the above image are 26 clue numbers provided, well above the minimum of 17 required for a unique solution.

Traditional Sudoku solving strategies involve working rules with the rows, column and boxes to uncover the next clues and eventually finishing the puzzle. Some Sudoku can be solved using just a few of the simple rules but other example require the a set of rules including the "Swordfish" and "X-Y Wings". The more advanced rules are context sensitive and require considerable mental dexterity to apply consistently. Using a solver the logic of the problem is described, clue numbers inserted and the solver does the rest.

Applying the simpler rules to the above puzzle generates 17 further clues but then gets stuck.

3 ? 1 2 ? 9 4 ? 7	2 9 ? ? 4 6 ? ? ?	5 4 ? ? 1 ? 9 ? ?
1 7 ? 9 3 5 6 2 ?	? ? 5 ? ? ? 9 ? ?	? ? 9 ? 7 ? ? 5 1
8 1 2 5 9 3 7 4 6	? ? ? 8 1 ? ? ? 9	? 9 5 ? ? 4 1 ? 8

Taking a different approach we can transcribe the Sudoku into a set of logical expressions in the SMT-LIB language and send to a general purpose solver to come up with an answer. 

The starting input would be 81 numbers between 0 and 9. The 0 represents an unsolved number, the other digits are clues.

#t2 118 Fiendish f63.txt

301200500

200046010

000000900

170005000

030000070

000900051

002000000

090810004

006009108

Building SMT-LIB file

The cells in the puzzle are represented in the solver as v0 to v80. First we have a couple of set up lines then we declare 81 lines of integer values 

(set-logic LIA)

(set-option :produce-models true)

(set-option :produce-assignments true)

(declare-const V0 Int)

(declare-const V1 Int)

(declare-const V2 Int)

..... up to V80

Each cell can only have the numbers 1 to 9. Read this as V0 must be a whole number greater than 0 and less than 10.

(assert (and (> V0 0) (< V0 10)))

(assert (and (> V1 0) (< V1 10)))

(assert (and (> V2 0) (< V2 10)))

..... up to V80

Include the known values.

(assert (= V0 3 ))

(assert (= V2 1 ))

(assert (= V3 2 ))

(assert (= V6 5 ))

(assert (= V9 2 ))

..... for each of the clue numbers provided

For each row, column and sub-box set the constraints that the values must be distinct and unique

(assert (distinct V0 V1 V2 V3 V4 V5 V6 V7 V8 ))

(assert (distinct V9 V10 V11 V12 V13 V14 V15 V16 V17 ))

(assert (distinct V18 V19 V20 V21 V22 V23 V24 V25 V26 ))

....

(assert (distinct V60 V61 V62 V69 V70 V71 V78 V79 V80 ))

Finally trigger the solver and ask for the values found.

(check-sat)

(get-value (V0 V1 V2 V3 V4 V5 V6 V7 V8 V9 V10 V11 V12 V13 V14 V15 V16 V17 V18 V19 V20 V21 V22 V23 V24 V25 V26 V27 V28 V29 V30 V31 V32 V33 V34 V35 V36 V37 V38 V39 V40 V41 V42 V43 V44 V45 V46 V47 V48 V49 V50 V51 V52 V53 V54 V55 V56 V57 V58 V59 V60 V61 V62 V63 V64 V65 V66 V67 V68 V69 V70 V71 V72 V73 V74 V75 V76 V77 V78 V79 V80 ))

(exit)

If the puzzle can be solved the output would be "sat" followed by the values for each square. The solver takes about 0.2s on a MacBookPro 2011 with a 2.2Ghz Core i7

sat

( (V0 3)

  (V1 6)

  (V2 1)

  (V3 2)

  (V4 9)

  (V5 8)

  (V6 5)

  (V7 4)

  (V8 7)

  (V9 2)

  (V10 5)

... up to V80

These answers can then be loaded into a table giving the answer ...

3 6 1 2 5 9 4 8 7	2 9 8 7 4 6 3 5 1	5 4 7 8 1 3 9 6 2
1 7 4 9 3 5 6 2 8	6 3 5 1 8 2 9 7 4	2 8 9 4 7 6 3 5 1
8 1 2 5 9 3 7 4 6	4 6 3 8 1 7 5 2 9	7 9 5 6 2 4 1 3 8

Going Supersize

Problems with just 55 unknowns are useful for proving a methodology but don't stretch the technique.   Taking a step up to a Giant SudokuX is more of a test with 367 cells. The giant SudokuX has 5 overlapping Sudokus, the inner puzzle sharing 3*3 corners with the outer puzzles. The red cells with x are unused.

Using a sequential cell numbering schema the input for the integer SMT solver can be generated with a similar script as a normal sudoku puzzle.

Each cell is defined as an integer and included in a row, column and box constraint and if is a clue cells, set with a value. For Example cell 261 of this puzzle is in the row starting cell 258, column starting cell 135 and box starting cell 261. In this puzzle happens to be set as a clue number value 1.

From the .SMT2 file looking at just the lines that involve cell V261 we see

$ grep V261 DT_29Feb.smt2

(declare-const V261 Int)

(assert (and (> V261 0) (< V261 10)))

(assert (= V261 1 ))

(assert (distinct V258 V259 V260 V261 V262 V263 V264 V265 V266 )) ; line 258 1

(assert (distinct V135 V156 V177 V198 V219 V240 V261 V282 V303 )) ; line 135 21

(assert (distinct V261 V262 V263 V282 V283 V284 V303 V304 V305 )) ; box 261 21 21

(get-value (V0 V1 V2 V3 V4 V5 V6 V7 V8 V12 V13 V14 V15 V16 V17 V18 

.....

V218 V219 V220 V221 V222 V223 V224 V237 V238 V239 V240 V241 V242 V243 V244 V245 V252 V253 V254 V255 V256 V257 V258 V259 V260 V261 V262 V263 

......

V436 V437 V438 V439 V440 ))

When run through the solver and processed into an html table we can see the result in less than 2 seconds of solver time.

$ ./sudoku_GiantX_smt2.pl < DT_29Feb.csv | grep -v '#' | time ../solver_m5 | ./sudoku_GiantX_smt2.pl > DT_29Feb_m5.html 

        1.82 real         1.77 user         0.03 sys

7 3 6 9 5 2 1 8 4	1 9 4 7 8 6 2 3 5	8 5 2 3 4 1 7 9 6		8 3 2 1 9 7 5 4 6	1 7 4 2 5 6 8 3 9	9 6 5 8 3 4 1 2 7
2 7 9 3 4 1 5 6 8	3 6 8 5 2 9 4 1 7	5 1 4 6 7 8 2 3 9		9 6 8 4 1 3 2 7 5	3 2 5 6 8 7 4 9 1	7 4 1 5 9 2 6 8 3
8 1 3 6 9 7 4 2 5	9 5 2 8 4 3 6 7 1	4 6 7 1 2 5 9 8 3	2 8 1 9 6 3 4 5 7	3 5 9 7 8 4 6 2 1	7 6 2 9 1 3 5 4 8	4 1 8 2 5 6 3 7 9
		3 1 8 5 7 4 2 9 6	7 2 6 8 1 9 5 3 4	4 9 5 2 3 6 1 7 8
8 1 5 2 4 6 9 7 3	7 9 4 3 8 1 2 5 6	6 3 2 7 5 9 8 4 1	1 9 8 6 4 2 3 7 5	5 4 7 8 1 3 9 6 2	2 9 3 6 7 4 5 1 8	6 1 8 2 5 9 4 3 7
7 3 4 6 8 1 5 2 9	9 6 8 5 3 2 1 4 7	2 1 5 4 9 7 3 6 8		4 5 1 7 3 6 2 8 9	9 2 7 4 8 5 3 6 1	8 6 3 1 9 2 7 4 5
4 9 8 1 5 7 3 6 2	6 7 5 4 2 3 8 1 9	1 2 3 9 8 6 5 7 4		1 9 4 6 2 5 3 7 8	7 3 2 8 4 9 1 5 6	5 8 6 3 7 1 9 2 4

A couple of counter examples of broken Sudoku are presented to the solvers which reject them as "unsat". Both the Math5SAT and Z3 solver are able to complete the samples of this problem.

Going Super Supersize

Daily Mail Giant Samurai Sudoku 

The DM paper had special puzzle section that included a "Giant Samurai Sudoku" consisting of 8 interlocked puzzles. The pre-processing script from the Giant Sudoku above was quickly adapted to feed the solvers with the new puzzle. In this example the  Z3 solver  took about 1.56s and the Math5SAT about 12 seconds on a 2012 MacBook Pro laptop.

4 6 2 7 8 1 3 5 9	5 3 9 2 6 4 8 7 1	8 1 7 3 9 5 2 4 6		4 9 8 1 5 6 2 7 3	2 5 6 3 7 9 1 8 4	3 1 7 8 2 4 9 6 5
9 4 8 1 2 3 6 7 5	1 2 7 9 5 6 4 8 3	6 5 3 7 8 4 1 2 9		6 3 4 5 2 7 9 8 1	7 1 8 9 6 3 5 4 2	2 5 9 4 8 1 7 3 6
8 1 7 5 3 4 2 9 6	6 9 5 7 1 2 3 4 8	4 3 2 9 6 8 5 7 1	5 6 7 1 2 3 8 9 4	8 1 9 7 4 5 3 6 2	6 2 7 8 3 1 4 9 5	5 4 3 6 9 2 1 7 8
		1 8 9 2 4 3 7 5 6	4 7 2 6 5 8 9 3 1	5 3 6 9 7 1 2 8 4
3 9 8 7 4 2 5 1 6	5 4 2 6 3 1 8 7 9	6 1 7 8 9 5 3 2 4	2 8 9 3 4 6 7 1 5	4 5 3 1 2 7 6 9 8	8 7 9 4 6 5 2 3 1	1 2 6 9 3 8 7 4 5
1 8 9 4 6 7 2 3 5	4 5 3 9 2 8 7 1 6	7 6 2 5 3 1 4 8 9		3 4 1 9 8 2 5 7 6	5 8 7 3 4 6 9 1 2	6 9 2 5 1 7 4 8 3
9 5 3 8 7 1 6 2 4	2 6 4 3 9 5 1 8 7	1 7 8 2 4 6 9 5 3	4 5 6 7 3 9 1 8 2	2 3 9 8 1 5 7 6 4	6 5 4 7 9 3 1 2 8	8 7 1 2 6 4 3 5 9
		4 9 1 7 6 5 3 8 2	3 7 5 2 9 8 6 4 1	6 2 8 3 4 1 5 9 7
8 6 2 4 9 5 3 1 7	4 7 3 2 1 6 5 9 8	5 1 9 8 3 7 6 2 4	8 2 3 9 6 4 5 1 7	4 7 6 1 5 2 9 8 3	1 8 3 7 6 9 2 4 5	2 5 9 3 8 4 6 7 1
9 3 1 2 5 4 7 8 6	6 8 2 7 3 9 1 4 5	4 7 5 1 6 8 2 9 3		8 9 1 7 3 4 6 2 5	5 7 6 9 2 8 3 1 4	4 2 3 5 1 6 7 9 8
1 7 9 5 4 3 6 2 8	8 2 4 9 6 1 3 5 7	3 5 6 7 8 2 9 4 1		3 1 8 5 6 7 2 4 9	6 5 2 4 9 1 8 3 7	9 4 7 8 3 2 1 6 5

Going Super Blow out Supersize

On the 2020 May bank holiday the DM published a Union Jack Giant Sudoku consisting of 13 interleaved puzzles. The Giant X script was lightly modified to account for the new arrangement and .. Boom solved in less than 5.06s using MathSAT solver. The colour squares had no special significance.

May Bank holiday 2020 Union Jack Giant Sudoku.

Alternative Super Sudoku 4x3

Instead of going larger some variants of sudoku become more complex. For example SuperSudoku4x3 uses a 12 by 12 grid with rows, columns and sub square each requiring the numbers 1..12. 

The text input encoding for this variant uses a coma separated text file.

#SudokuSuper4x3 dm ss43_0893.txt

1,0,0,0,12,0,0,0,0,0,8,0

3,0,0,0,1,11,10,4,9,2,0,0

2,5,0,0,6,0,0,8,1,4,0,0

0,0,1,0,0,10,0,12,0,0,0,8

0,6,7,0,0,0,0,0,0,0,0,10

0,0,8,0,0,6,0,0,0,1,2,0

8,11,0,0,0,4,0,9,0,0,0,0

0,4,12,6,11,0,5,3,0,0,0,0

9,0,0,0,0,2,12,0,11,8,0,7

5,10,0,1,0,0,4,0,0,0,6,0

6,9,11,12,0,0,0,1,8,0,0,0

0,8,0,0,5,9,0,0,0,11,0,12

The solver rules generation is essentially similar to other sudoku building rules for each unknown and known value with dependancy lines for each row, column and sub-square.  Passed to a solver the results are returned and processed into an .html table.

_1 _7 _4 11 _3 12 _6 _8 _2 _5 _9 10	12 _5 _9 _2 _1 11 10 _4 _6 _3 _7 _8	10 _6 _8 _3 _9 _2 _7 _5 _1 _4 12 11
11 _2 _1 _4 12 _6 _7 _9 10 _3 _8 _5	_9 10 _3 12 _2 _1 _8 _5 _4 _6 11 _7	_6 _7 _5 _8 _4 _3 11 10 12 _1 _2 _9
_8 11 10 _2 _7 _4 12 _6 _9 _1 _5 _3	_7 _4 _1 _9 11 _8 _5 _3 10 _2 12 _6	_5 12 _3 _6 _2 10 _9 _1 11 _8 _4 _7
_5 10 _3 _1 _6 _9 11 12 _4 _8 _2 _7	_8 12 _4 11 _3 _7 _2 _1 _5 _9 _6 10	_7 _9 _6 _2 _8 _5 10 _4 _3 11 _1 12

Count of Values check = 1=12,10=12,11=12,12=12,2=12,3=12,4=12,5=12,6=12,7=12,8=12,9=12,

Sudoku_5x5 :

This form of sudoku has 5*5 cells each with the digits and letters 0..9 K..Z.

Internally the letters are translated to consecutive integers 10..25 and back again for output.

The input encoding is 

#gs555 Journal_4Nov2021 gs555_001.txt

N6005 00P04 0K000 80Q90 000X0 

0000M 00000 90000 00000 60O00 

00000 79K08 0000T 0Z000 00050 

4RQ08 N00SL 00V0W K000M 00000 

V0300 Y0X00 27005 00R04 P0MN0 

00000 0RUM6 00080 N0007 QX2W0 

0Y000 0000K 04T00 00V6R 7M300 

0W00P ZXL00 037S0 0U00O 00Y00 

00007 10000 00XRN 0S058 KP000 

L00V0 30500 00W0P M940X S0U00 

OL000 0T00V 0600S 00Z0W 00409 

000TQ 00200 0WN70 0M0X9 0L0R0 

0001U 0005Z 00000 23OSK X0000 

00000 0M000 QYKZ0 L4P00 01N00 

7K00S 48000 PX0V0 U0501 O0020 

X00RT 00607 KZ090 00000 0Q000 

00850 0S030 L000V 0Q0N0 R0000 

03000 WVRK0 000P0 Z0Y00 08500 

0470W PY090 N20MQ 00L10 300Z0 

00M00 OZ00N 01030 0V000 04X0Y 

0050V 00100 W0Z0Y 0000T 90000 

M0Y0R 00000 009Q0 068O0 0K700 

01P30 0LM70 00U08 W5X00 0OS00 

080X0 06OQ0 0005L 0090Z 2WP00 

0S0Q0 00049 0O602 0P0ML 03008 

and the result comes out as 

Interestingly these Sudoku with more choices per cell takes much longer to solve than the puzzles with more cells but a limited value range. The 5x5 puzzle here took 214.60 seconds where as the MayBankHoliday Sudoku took, using the same solver,  just  0.27s seconds.

% ../../solver_z3 --version

Z3 version 4.8.12 - 64 bit

Magidoku and Quasi-Magic Sudokus

There are a couple of variants of sudokus that are more complex than standard sudokus but use the same 9 * 9 grid pattern. Magidokus start with regular sudoku rules then add the extra constraints that each 3*3 sub square must have rows and columns must add up to 15. Quasi-Magic Sudokus, start with regular sudoku rules, then add the extra constraints that each 3*3 sub square must have rows, columns and diagonals that add to any of 13,14,15,16, or 17. Both these variations can be solved in the same way as above with the addition of some extra constraint lines.  What looks interesting here is having more rules and much fewer starting clues. 

For example this example of a quasi-magic sudoku has just 4 starting clues 

Encoded with  . representing 0 as  

#Quasi-MagicSoduko Puzzle G qms_009.txt

*.......................5.............................7..6..........3............./

is solved in about 24s using MathSat5

9 1 5 2 4 7 6 8 3	4 2 7 8 6 3 1 9 5	6 8 3 1 5 9 7 2 4
7 2 4 3 6 8 5 9 1	6 1 9 7 5 2 3 8 4	5 3 8 9 4 1 2 6 7
1 7 6 8 5 2 4 3 9	5 4 8 9 3 1 2 7 6	3 9 2 4 7 6 8 1 5

In each of the 9 sub-boxes  the rows, columns and diagionals all add up to between  13 to 17 inclusive. The 72 extra constraint lines are in this format :

(assert (and (< 12 (+ V61 V70 V79 )) (> 18 (+ V61 V70 V79 ))))

For Magidoku 54 extra constraint lines are added with this format.

(assert (= 15 (+ V0 V9 V18 )))

References

Programming Z3 Sudoku section from Section 8.1 page 139

Some articles about it: Building a Sudoku Solver with SAT, Tjark Weber.  A SAT-based Sudoku Solver, Ines Lynce,

Pattern-Based Constraint Satisfaction and Logic Puzzles - Denis Berthier
Joel Ouaknine, Sudoku as a SAT Problem, Gihwon Kwon, Himanshu Jain, Optimized CNF Encoding for Sudoku Puzzles.

Tony Forbes, Sudoku and Magic Squares 

Man page

Run sudoku_smt.pl < text of Sudoku puzzle to generate input file for SMT-Lib solver

    or generate html table of results head z3 from a SMT solver output

Each cell value can be 1..9 only repeats NOT allowed.

Sudoku puzzle Input as follows (Can have . instead of 0 in input)

#dm 1402 F1 Puzz 

900081600

600904005

401000300

200708010

700010904

060400700

007000401

590002037

000530006

        

Also accepts these formats and puzzles (no trailing spaces pls)

        The keyword after the # and leading characters determins the puzzle type

        

#Sudoku dm 1402 F1 Puzz

900081600600904005401000300200708010700010904060400700007000401590002037000530006

    

#Sudoku dm 1402 F1 Puzz

9...816..6..9.4..54.1...3..2..7.8.1.7...1.9.4.6.4..7....7...4.159...2.37...53...6

        

#Magidoku  PuzzleE  magi_001.txt Subsquares c,r,d add to 15

+...........62.............6..1.....................5..5.............36.........../

#Quasi-MagicSudoku TF0378fq Subsquares c,r,d add to any of 13,14,15,16,17

*..4................8.............4.....2.9.....3.............4................6../

        

to generate an SMT2 input file

Internal Variables are

    $tv{ 0 .. 80 }

......

OR Process results from solver in the following format

    sat

    ( (V0 9)

    (V1 7)

    (V2 5)

    (V3 3)

    ....

to generate an html table as output

EOP

*** Update 05 Nov 2024

Q: Can chatGPT solve all sudoku ?

ChatGPT:  ChatGPT can help solve many Sudoku puzzles by applying a logical, step-by-step approach, but it does have some limitations:

Logical Strategies and Explanation: ChatGPT can walk you through various solving techniques (like Naked Singles, Hidden Pairs, X-Wing, etc.) and apply them in a logical order to solve the puzzle. For many standard Sudoku puzzles, this method is effective and often enough to reach a solution.

Complexity and Advanced Techniques: For highly complex puzzles, such as those requiring advanced techniques (e.g., Swordfish, Jellyfish, or even more intricate techniques used in extreme Sudoku variants), ChatGPT may need external support, like an SMT solver or specific backtracking algorithms, which require computational logic and precision.

Consistency and Verification: ChatGPT may not perfectly track all the placements or logic steps in real-time without a computational system in place. It’s designed for language and reasoning but lacks the persistent, systematic memory needed to ensure that every logical deduction is correct and free of contradictions.

No Access to Real-Time Calculations: In this chat-only environment, ChatGPT doesn't directly execute code to solve Sudoku with brute-force algorithms (such as backtracking or SMT solvers) or check constraints dynamically. It can outline these methods in code (like Python or Z3), which you can run in a suitable programming environment.

Conclusion

In short, while ChatGPT can explain and help solve many standard Sudoku puzzles through logical reasoning and pattern recognition, it may not be able to solve all Sudoku puzzles independently without computational assistance, especially those requiring extensive backtracking or advanced constraints. However, with external tools, such as an SMT solver or a Sudoku-solving algorithm, it could solve even the most challenging puzzles reliably.